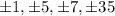Answer:
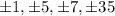
Explanation:
Given: A new company estimates its total profit as
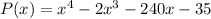 , where P is in hundreds of dollars and x is the number of months elapsed since the company’s start-up.
, where P is in hundreds of dollars and x is the number of months elapsed since the company’s start-up.
The coefficient of the leading term (a)= 1
The constant term = 35
The factors of 35 (b)=
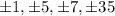
By rational root theorem , we have
The rational zeros
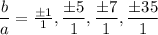
Hence, the values of x until the company breaks even =