The Lagrangian is
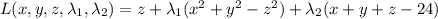
with partial derivatives (set equal to zero) yielding
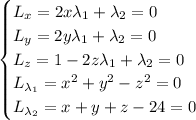
Subtracting the second equation from the first gives

So in the fourth and fifth equations, we have
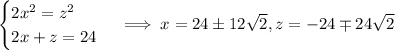
There are then two critical points for
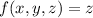
at
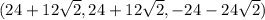
and
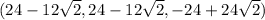
.
Clearly,
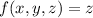
attains a local minimum at the first point of
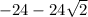
, and a local maximum at the second point of
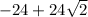
.