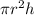Answer:
Volume of cylinder =
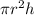
Explanation:
Given : A cylinder fits inside a square prism.
To find : The volume of cylinder
Solution : Refer the attached graph.
Area of circle =
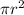
Area of square =
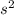
Side of square = diameter of circle=
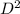
Diameter = 2r
∴ Area of square=
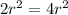

Area of circle is
 of area of square.
of area of square.
Volume is always = area × height
Volume of prism = Area of square × h =
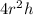
Volume of cylinder = Area of circle × h =
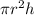
Now, rate
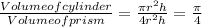
⇒Volume of cylinder is
 of Volume of prism.
of Volume of prism.
Volume of Cylinder =
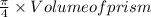
Volume of cylinder =
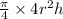
Volume of cylinder =