Question

Simplify completely quantity x squared plus 4 x minus 45 all over x squared plus 10 x plus 9 and find the restrictions on the variable. A quantity x minus 5 over quantity x plus 1, x ≠ −1, x ≠ −9 B quantity x minus 5 over quantity x plus 1, x ≠ −1, x ≠ 5 C quantity x plus 5 over quantity x plus 1, x ≠ −1, x ≠ −9 D quantity x plus 5 over x plus 1, x ≠ −1, x ≠ 5, and i know that b is wrong

Answer 1

This can be factored into (x+9)(x+5)/(x+9)(x+1)
once simplified, it's (x+5)/(x+1)
The denominator cannot be negative, so x≠-1

Therefore, the answer is C.

Answer 2

Option: A is correct (quantity x minus 5 over quantity x plus 1, x ≠ −1, x ≠ −9)

Explanation:

We are asked to simplify the expression:

`=(x^2+4x-45)/(x^2+10x+9)`

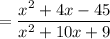
We know that this question could also be written as:

`=(x^2+9x-5x-45)/(x^2+9x+x+9)`

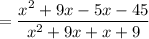
since on using the method of splitting the middle term.

`=(x(x+9)-5(x+9))/(x(x+9)+1(x+9))\\ \\=((x-5)(x+9))/((x+1)(x+9))`

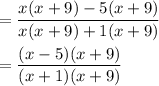
Also x≠ -9 and x≠-1 (since by looking at the denominator term the denominator has to be non zero)

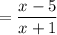`=(x-5)/(x+1)` ; x≠ -9 and x≠-1

Hence, option A is correct.