Question

The perimeter of a square is 56 cm. What is the approximate length of its diagonal?

Answer 1

s = 56 cm
s / 4

= 56/4
= 14.0 cm

Answer 2

19.8

Explanation:

To find out the length of the diagonal of a square, first we need the length of it sides. We will get this information from the perimeter.

We calculate the perimeter of a square adding up the length of the 4 sides. As all the sides of a square are equal, we just take one side and multiply it by four.

So, if the perimeter is 56 cm, that means 56 = 4*L, where L represents the length of the sides. If we want to know the value of L, we have to divide by 4 on both sides:

56 = 4*L

56/4 = 4/4*L

14 = L

Now we can find out the length of the diagonal using the Pythagorean equation

`\fbox {\textbf{Pythagorean equation}:}` The square of the length of the hypotenuse (the side opposite the right angle) of a right triangle is equal to the sum of the squares of the two legs (the two sides that meet at a right angle)

In this case, the hypotenuse is the diagonal we want to find out and the legs are the two sides of the square.

So, we have

`D^2 = L^2 + L^2`

`D^2 = 14^2 + 14^2`

`D^2` = 392

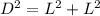
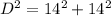
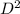`D = √(392)`

D = 19.8