Question

2. Triangles ABC and A1B1C1 are similar. Calculate the areas of these triangles if:

Answer 1

In the similar triangles

`\begin{gathered} (P_1)/(P_2)=(s_1)/(s_2) \\ (A_1)/(A_2)=((s_1)/(s_2))^2 \end{gathered}`

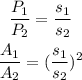
Since the ratio between the perimeters of 2 similar triangles, ABC and A1B1C1 is 4/5

By using the first rule above, the ratio between their sides is 4/5

`\begin{gathered} (P_(ABC))/(P_(A_1B_1C_1))=(4)/(5) \\ (s_(ABC))/(s_(A_1B_1C_1))=(4)/(5) \end{gathered}`

Since the sum of their area is 410 cm^2, then

`\begin{gathered} A_(ABC)+A_(A_1B_1C_1)=410 \\ A_(A_1B_1C_1)=410=A_(ABC) \end{gathered}`

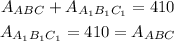
By using the 2nd rule above

`(A_(ABC))/(A_(A_1B_1C_1))=((4)/(5))^2=(16)/(25)`

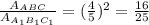
Substitute Area of triangle A1B1C1 by 410 - ABC

`(A_(ABC))/(410-A_(ABC))=(16)/(25)`

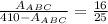
By using the cross-multiplication

`\begin{gathered} 25* A_(ABC)=16*(410-A_(ABC)) \\ 25A_(ABC)=6560-16A_(ABC) \end{gathered}`

Add 16A (ABC) to both sides

`\begin{gathered} 25A_(ABC)+16A_(ABC)=6560-16A_(ABC)+16A_(ABC) \\ 41A_(ABC)=6560 \end{gathered}`

Divide both sides by 41

`\begin{gathered} (41A_(ABC))/(41)=(6560)/(41) \\ A_(ABC)=160cm^2 \end{gathered}`

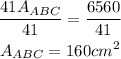
Subtract it from 410 to find the area of triangle A1B1C1

`\begin{gathered} A_(A_1B_1C_1)=410-160 \\ A_(A_1B_1C_1)=250cm^2 \end{gathered}`

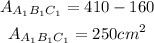
The areas of the 2 triangles are 160 cm^2 and 250 cm^2