Question

In 5 years, Dad will be three times as old as his daughter Jill will be then. If the sum of their present ages is 50, how old are they now? If y + 5 is Jill's age five years from now, which of the following equations could be used to solve the problem?

Answer 1

First, we know (D is dad, J is Jill) that D+J=50.
Second, in 5 years D will be 3 times as old so
(D+5)= 3*(J+5)
Moving on, if we know D+J=50 then D=(50-J) is true.Taking that relationship and substituting for D in the other equation, it becomes
50 - J + 5 = 3 * (J + 5)
Then, it becomes 50 - J + 5 = (3 * J) + (3 * 5)
Then, 55 - J = (3 * J) + 15
Then, 55 - 15 = (3 * J) + J
which becomes 40 = 4*J

Answer 2

Dad's current age is 40 years and Jill's age is 10 years.

Explanation:

Let Dad's current age be = x

Let Jill's current age be = y

The sum of their present ages = 50

We get :
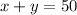`x+y=50` or
`x=50-y`

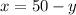
In 5 years, Dad will be three times as old as his daughter Jill will be then.

`x+5=3(y+5)`

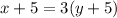
Putting the value of x here;

`50-y+5=3y+15`

=>
`55-y=3y+15`

=>
`3y+y=55-15`

=>
`4y=40`

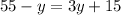
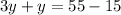
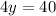
y = 10

And
`x=50-10`

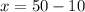
x = 40

Hence, dad's current age is 40 years and Jill's age is 10 years.