Answer:
16,400 miles
Step-by-step explanation:
Kepler's third law states that the ratio between the cube of the distance of a satellite from its planet and the square of its orbital period is constant for all the satellite orbiting around that planet:
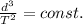
where d is the distance of the satellite from the planet and T is the orbital period.
By applying this law to the Moon and the other satellite of this problem, we can write
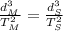
where
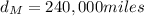 is the distance of the Moon from the Earth,
is the distance of the Moon from the Earth,
 is its orbital period,
is its orbital period,
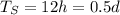 is the orbital period of the satellite. Re-arranging the equation and replacing the numbers, we can find dS, the distance of the satellite from the Earth:
is the orbital period of the satellite. Re-arranging the equation and replacing the numbers, we can find dS, the distance of the satellite from the Earth:
![d_S=\sqrt[3]{(d_M^3 T_S^2)/(T_M^2)}= \sqrt[3]{((240,000)^3 (0.5)^2)/((28)^2)}=16,400 miles](https://img.qammunity.org/2018/formulas/physics/high-school/hyedzrr6kt4aldnl20oxu63sbvmhlvur3n.png)