Answer:
Option A and D are correct
(–8, 8) and (2, 2), (–2, 1) and (3, –2)
Explanation:
Parallel line:
In parallel lines, the two lines have the same slope and will never intersects.
Using the slope formula:
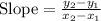 ....[1]
....[1]
As per the statement:
A line has a slope of -3/5.
We have to find which ordered pairs could be points on a parallel line.
A.
(–8, 8) and (2, 2)
Substitute in [1] we have;
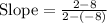
⇒
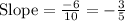
Similarly for:
B.
(–5, –1) and (0, 2)
Substitute in [1] we have;
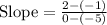
⇒
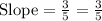
C.
(–3, 6) and (6, –9)
Substitute in [1] we have;
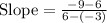
⇒
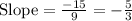
D.
(–2, 1) and (3, –2)
Substitute in [1] we have;
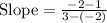
⇒
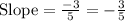
E.
(0, 2) and (5, 5)
Substitute in [1] we have;
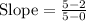
⇒
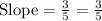
Therefore, the ordered pairs could be points on a parallel line are:
(–8, 8) and (2, 2)
(–2, 1) and (3, –2)