Question

Given: parallel lines are crossed by a transversal line. What is the value of x?

Answer 1

The angles shown are same side interior angles. They add to 180 degrees

x+100 = 180
x+100-100 = 180-100
x = 80

Therefore, the answer is 80

Answer 2

The value of x is, 80 degree.

Explanation:

Given the statement:

Parallel lines are crossed by a transversal line.

Interior angles:

If parallel lines are cut by a transversal, then same-side interior angles are supplementary(i.e 180 degree)

From the given figure:

`100^(\circ)` and
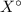`X^(\circ)` are on the same side.

By definition of interior angle:

`100^(\circ)+X^(\circ)=180^(\circ)`

Subtract 100 degree from both sides we have;

`X = 80^(\circ)`

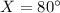
Therefore, the value of x is, 80 degree.