Question

What is the equation of the line passing through the points (2, –1) and (5, –10) in slope-intercept form?

Answer 1

slope intercept is m and m=-3
y intercept is b and b=5

Answer 2

The equation of the line passing through the points (2, –1) and (5, –10) is y = -3x + 5 .

Explanation:

The equation of a slope is given by

`(y - y_(1)) = (y_(2)-y_(1))/(x_(2)-x_(1))(x - x_(1))`

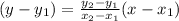
As the line passing through the points (2, –1) and (5, –10) .

Put all the values in the above

`(y - (-1)) = (-10-(-1))/(5-2)(x - 2)`

`(y + 1) = (-10+1 )/(5-2)(x - 2)`

`(y + 1) = (-9)/(3)(x - 2)`

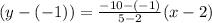
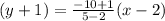
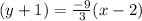
3y + 3 = -9x -9 × -2

3y + 3 = -9x + 18

3y = -9x + 18 -3

3y = -9x + 15

Simplify the above

3y = 3 (-3x + 5)

y = -3x + 5

Therefore the equation of the line passing through the points (2, –1) and (5, –10) is y = -3x + 5 .