Question

Jessica cannot remember the correct order of the six digits in her ID number. She does remember that the ID number contains the digits 1, 0, 7, 3, 9, 5. What is the probability that the first five digits of Jessica’s ID number will all be odd numbers?

Answer 1

There is only one even number (0), so this probability equals the probability that the ID number ends with 0. One of the 6 digits has to come last, so the probability is 1 out of 6, ie., 1/6

Answer 2

0.167

Explanation:

Given : The six digits ID number contains the digits 1, 0, 7, 3, 9, 5.

To Find: What is the probability that the first five digits of Jessica’s ID number will all be odd numbers?

Solution:

Odd numbers = 1,7,3,9,5 = 5

Total numbers = 1, 0, 7, 3, 9, 5 =6

So, probability that the first digit is odd =
`(5)/(6)`

Now remaining odd numbers = 4

Total remaining numbers =5

So, probability that the second digit is odd =
`(4)/(5)`

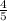
Now remaining odd numbers = 3

Total remaining numbers =4

So, probability that the third digit is odd =
`(3)/(4)`

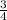
Now remaining odd numbers = 2

Total remaining numbers =3

So, probability that the fourth digit is odd =
`(2)/(3)`

Now remaining odd numbers = 1

Total remaining numbers =2

So, probability that the fifth digit is odd =
`(1)/(2)`

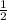
So, probability that the first five digits of Jessica’s ID number will all be odd numbers:

=
`(5)/(6) * (4)/(5) * (3)/(4)* (2)/(3) * (1)/(2)`

=
`0.167`

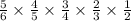
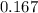
Hence the probability that the first five digits of Jessica’s ID number will all be odd numbers is 0.167