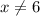Question

Identify the restrictions on the variable x^2+3x+2/x^2-4x-12

Answer 1

x^2 - 4x -12 ≠ 0
Let's say it's equal to 0
Δ = b^2 -4ac
(-4)^2 -4(-12)
16 + 48
64

x1, x2 = -b ± √Δ / 2a
-(-4) ± √64 / 2
4 ± 8 / 2
x1 = 4+8/2, x2 = 4-8/2
x1 = 12/2 = 6, x2 = -4/2 = -2

So x can't be 6 or -2!

Answer 2

The restrictions on the variable x in the expression
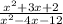`(x^2+3x+2)/(x^2-4x-12)` is
`x\\eq6`

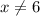
Explanation:

Given : Expression
`(x^2+3x+2)/(x^2-4x-12)`

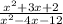
To find : Identify the restrictions on the variable ?

Solution :

First we simplify the expression,

`(x^2+3x+2)/(x^2-4x-12)`

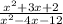
Applying middle term split to factor,

`=(x^2+2x+x+2)/(x^2-6x+2x-12)`

`=(x(x+2)+1(x+2))/(x(x-6)+2(x-6))`

`=((x+2)(x+1))/((x-6)(x+2))`

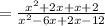
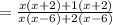
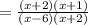
Cancel the like term in Nr. and Dr.,

`=(x+1)/(x-6)`

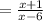
Now, To find restriction for x set each polynomial or term in the denominator to cannot equal to 0.

So, Put denominator = 0

`x-6=0`

`x=6`

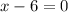
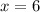
Which means the restriction is
`x\\eq6`

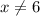
Therefore, The restrictions on the variable x in the expression
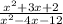`(x^2+3x+2)/(x^2-4x-12)` is
`x\\eq6`