Question

Prove that sin20sin40sin60sin80=3/16

Answer 1

We'll use the following properties of sine and cosine to prove this:


`sin(a)\cdot sin(b) = \frac12(cos(a-b) - cos(a+b))`


`cos(a)\cdot cos(b) = \frac12(cos(a+b) + cos(a-b))`


`cos(180+a) = cos(180-a)`

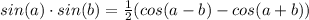
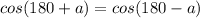
Then it's just a matter of filling it in...

sin20sin40 * sin60sin80 = 1/2(cos20 - cos60) * 1/2 (cos20 - cos140) =

1/8( cos40 + 1 - cos160 - cos120 - cos40 - cos80 + cos80 + cos200) =

1/8(1 - cos160 - cos120 + cos200) =

1/8(1 - cos160 - cos120 + cos160) =

1/8(1 - cos120 ) = 1/8( 1 + 1/2 ) = 3/16