Question

Show and explain how replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solution

Answer 1

hope this helps
how replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solutions as the one shown. 8x + 7y = 39. 4x – 14y = –68.

The student is unable to show that (3, 4) is a solution of the given system. ... of that equation and a multiple of the other produces a system with the same solutions. ... Explain that when one equation in a system is replaced by the sum of that ...

Answer 2

Answer with Step-by-step explanation:

Consider the system of equation

`8x+7y=39`.....(1)

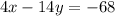`4x-14y=-68`...(2)

Now, multiply equation (1) by 2 and we get

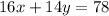`16x+14y=78`...(3)

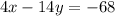`4x-14y=-68` ...(2)

Adding equation (3) with equation (2)

Then, we get

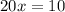`20x=10`..(4)

`x=(10)/(20)=(1)/(2)`

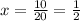
Now, substitute
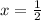`x=(1)/(2)` in equation (2)

`4((1)/(2))-14y=-68`

`2-14y=-68`

`-14y=-68-2=-70`

`y=(70)/(14)=5`

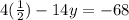
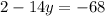
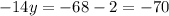
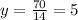
Equation (2) and equation (4) intersect at point (
`(1)/(2),5)`.

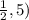Therefore, the solution of equation (2) and equation (4)

is (
`(1)/(2),5)`.

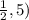Substitute
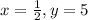`x=(1)/(2), y=5` in equation (1)

Then, we get

`8((1)/(2))+7(5)=4+35`

`4+35=39`

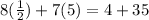
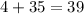
LHS=RHS

It means
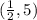`((1)/(2),5)`) is a solution of equation (1).

Substitute
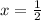`x=(1)/(2)` y=5 in equation (2)

Then, we get

`4((1)/(2))-14(5)=2-70=-68`

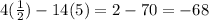
LHS=RHS

Therefore, the point
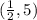`((1)/(2),5)` satisfied the equation (1) and equation (2).

Hence, the solution of equation (1) and equation (2) is (
`(1)/(2),5)`.

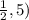We can say that solution of equation (1) and equation (2) and equation (2) and equation (4) is same.