Question

What are the possible numbers of positive real, negative real, and complex zeros of f(x) = 8x4 + 13x3 − 11x2 + x + 9?

Answer 1

Positive real zeros- 2 or 0

Negative real zeros - 2 or 0

Complex zeros-4 or 2 or 0

Explanation:

Answer 2

Answer: Positive real zeros- 2 or 0

Negative real zeros - 2 or 0

Complex zeros-4 or 2 or 0

Explanation:

Given: A fourth degree polynomial
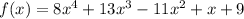`f(x)=8x^4+13x^3-11x^2+x+9` is arranged in descending order already .

We can see that it has two sign change from second to third term and then third to fourth ,so by Descartes rules of signs it has 2 or zero positive real roots.

Now
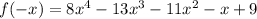`f(-x)=8x^4-13x^3-11x^2-x+9` [change signs of coefficient with odd degree of x]

Here we have two sign change from first to the second term and from fourth to the constant term.

Therefore by Descartes rules of signs f(x) has 2 or zero negative real roots.

As it is 4th degree polynomial so it can have 4 roots and complex roots occur in pair so f(x) can have 4 or 2 or 0 complex roots.