Answer:
Option A is correct .i.e., Always
Explanation:
There is a result of similarity of triangle which states that,
If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
Let ΔABC with ∠B = 90° and BD ⊥ AC
from above result,
ΔABD is similar to ΔCBD
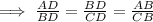
considering first equality we get,
BD² = AD . CD
This Proves that the altitude to the hypotenuse of a right triangle is always the geometric mean between the segments on the hypotenuse.
.
Therefore, Option A is correct.