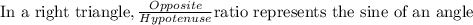Answer:
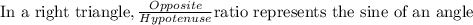
Explanation:
we have to tell the ratio represents the sine of an angle in a right triangle.
In right triangle ABC, the terms opposite, adjacent, and hypotenuse refer to lengths of sides as shown in attachment.
As, sine is defined as ratio of the opposite over hypotenuse.
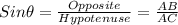
Hence,