Answer:
Right cone in a cylinder is inscribed in one another so that Cavalieri's principle can be applied to the volume of a sphere
Explanation:
We have to tell what figures must be inscribed in one another so that Cavalieri's principle can be applied to the volume of a sphere
Cavalieri's principle states that
If between the same parallel lines any two plane figures are drawn, and if in them, any straight lines being drawn equidistant from the parallel lines, the included portion of any one of lines are equal, the plane figures also equal to one another.
As, volume of the hemisphere is two-third of cylinder and that of the whole sphere is four-third of the volume of cylinder. The latter is
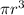, making the volume of the sphere
.
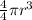Hence, right cone in a cylinder is inscribed in one another so that Cavalieri's principle can be applied to the volume of a sphere.