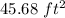Question

In the figure, the radius of the partial circle with center A is 4 feet.

The perimeter of the figure is ___ feet, and the area of the figure is ___ square feet.

Assume π = 3.14, and round your answers to the nearest hundredth.

Options for blank 1 are: 18.84, 24.50, 26.84, 75.36
Options for blank 2 are: 11.42, 22.84, 45.68, 53.68

Answer 1

first blank : 24.50 feet

second blank : 45.68 square feet

Explanation:

edmentum

Answer 2

Step 1

Find the perimeter of the figure

we know that

the perimeter of a circle is equal to the circumference

`C=2\pi r`

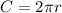
where

C is the circumference of the circle

r is the radius of the circle

we have

`r=4\ ft`

substitute

`C=2(3.14)4=25.12\ ft`

In the figure

the triangle ABC is a right triangle

Applying the Pythagoras Theorem find the length side CB

`CB^(2)=AB^(2) +AC^(2)`

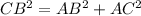
we have

`AC=AB=4\ ft`

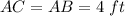
substitute the values

`CB^(2)=4^(2) +4^(2)`

`CB^(2)=32`

`CB=√(32)\ ft`

`CB=5.66\ ft`

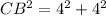
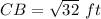
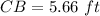
The perimeter of the figure is equal to
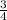`(3)/(4)` of the circumference plus the length side CB

so

`P=(3)/(4)25.12+5.66=24.50\ ft`

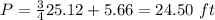
therefore

the answer Part a) is

the perimeter of the figure is
`24.50\ ft`

Step 2

Find the area of the figure

we know that

the area of a circle is equal to

`A=\pi r^(2)`

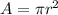
where

r is the radius of the circle

we have

`r=4\ ft`

substitute

`A=3.14(4^(2))=50.24\ ft^(2)`

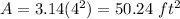
the area of the triangle ABC is equal to

`A=(1)/(2) bh`

in this problem

`b=BC=√(32)\ ft`

`h=BC/2=√(32)/2\ ft`

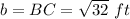
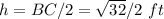
substitute the values

`A=(1)/(2)(√(32))(√(32)/2)=8\ ft^(2)`

the area of the figure is equal to
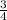`(3)/(4)` of the area of the circle plus the area of the triangle ABC

`A=(3)/(4)*50.24+8=45.68\ ft^(2)`

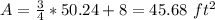
therefore

the answer Part b) is

the area of the figure is
`45.68\ ft^(2)`