Question

A gas of 19 mL at a pressure of 740 mmHg can be expected to change its pressure when its volume changes to 30. mL. Express its new pressure in units of atmospheres.

Answer 1

Answer: The new pressure will be 0.616 atm

Step-by-step explanation:

To calculate the new pressure, we use the equation given by Boyle's law. This law states that pressure is directly proportional to the volume of the gas at constant temperature.

The equation given by this law is:

`P_1V_1=P_2V_2`

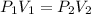
where,

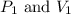`P_1\text{ and }V_1` are initial pressure and volume.

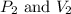`P_2\text{ and }V_2` are final pressure and volume.

We are given:

`P_1=740mmHg\\V_1=19mL\\P_2=?mmHg\\V_2=30mL`

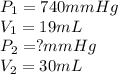
Putting values in above equation, we get:

`740mmHg* 19mL=P_2* 30mL\\\\P_2=468.66mmHg`

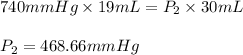
Converting this into atmospheres, we use the conversion factor:

1 atm = 760 mmHg

Now, converting the given quantity, we get:

`\Rightarrow (1atm)/(760mmHg)* 468.66mmHg=0.616atm`

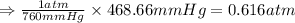
Hence, the new pressure will be 0.616 atm.

Answer 2

To solve this we assume that the gas is an ideal gas. Then, we can use the ideal gas equation which is expressed as PV = nRT. At a constant temperature and number of moles of the gas the product of PV is equal to some constant. At another set of condition of temperature, the constant is still the same. Calculations are as follows:

P1V1 =P2V2

P2 = P1V1/V2

P2 = 740mmhg x 19 mL / 30 mL

P2 = 468.67 mmHg = 0.62 atm