Question

What is the type of conic section given by the equation x^2 - 9y^2 = 900 and what is the domain and range?

Show the work if you can.

Answer 1

A conic section is a curve obtained by the intersection of the surface of a cone with a plane. A conic section can be a circle, a hyperbola, a parabola, and an ellipse.

For a circle, the general equation of a circle with center, (a, b), and a radius, r, is of the form

`(x-a)^2+(y-b)^2=r^2`

For a hyperbola, the general equation of a hyperbola with center (h, k), and a and b half the lengths of the major and the minor axis respectively is of the form.

`((x-h)^2)/(a^2) - ((y-k)^2)/(b^2) =1`

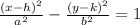
For a parabola, the general equation of a parabola with center (h, k), and a multiplier a is of the form

`y-k=a(x-h)^2`

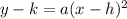
For an ellipse, the general equation of an ellipse with center (h, k), and a and b half the lengths of the major and the minor axis respectively.

`((x-h)^2)/(a^2) + ((y-k)^2)/(b^2) =1`

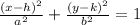
Given the equation

`x^2-9y^2=900`
It can be rewritten as

`((x-0)^2)/(900) - ((y-0)^2)/(100) =1 \\ \\ ((x-0)^2)/(30^2) - ((y-0)^2)/(10^2) =1`
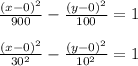
This gives an equation of a hyperbola with center (0, 0), half the length of the major axis = 30 and half the length of the minor segment = 10.

The domain of the equation is all real values of x.