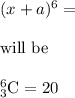Using Pascal's triangle
Number of terms Expression
1 = 1----------------------------
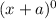
2 = 1 1----------------------------(x+a)
3 = 1 2 1-----------
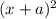
4= 1 3 3 1----------
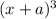
5= 1 4 6 4 1----------
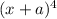
6= 1 5 10 10 5 1----------
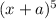
7= 1 6 15 20 15 6 1 ----------
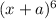
8= 1 7 21 35 35 21 7 1 ----------
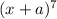
The meaning of
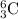 , is coefficient of fourth term of an expression having 7 terms.
, is coefficient of fourth term of an expression having 7 terms.
Using pascal Triangle value or coefficient of Fourth term of the expression