Question

Need help with indicial equation and ODEs

Answer 1

With


`y=\displaystyle\sum_(n\ge0)a_nx^(n+r)`

`y'=\displaystyle\sum_(n\ge0)(n+r)a_nx^(n+r-1)`

`y''=\displaystyle\sum_(n\ge0)(n+r)(n+r-1)a_nx^(n+r-2)`

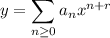
the singular ODE can be written as


`\displaystyle\sum_(n\ge0)\bigg[2(n+r)(n+r-1)+3(n+r)-1\bigg]a_nx^(n+r)+\sum_(n\ge0)\bigg[-2(n+r)(n+r-1)-3(n+r)\bigg]a_nx^(n+r-1)=0`

The first term of the second series admits the indicial equation. When
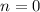
`n=0`, we have


`(-2r(r-1)-3r)a_0x^(r-1)=0\iff-2r^2-r=0\iffr^2+\frac12r=0`

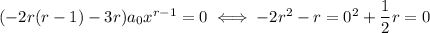
Factoring reveals two distinct roots at
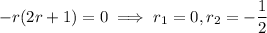
`-r(2r+1)=0\implies r_1=0,r_2=-\frac12` (in your case, swap
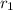
`r_1` and
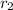
`r_2` before submitting).

Next, shift the index of the first sum so that it starts at
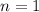
`n=1` by replacing
`n\mapsto n-1`, then consolidate the sums to get


`\displaystyle\sum_(n\ge1)\bigg[2(n+r-1)(n+r-2)+3(n+r-1)-1-2(n+r)(n+r-1)-3(n+r)\bigg]a_nx^(n+r-1)`

`=\displaystyle x^r\sum_(n\ge1)\bigg[-4n-4r\bigg]a_nx^(n-1)`

Setting
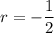
`r=-\frac12`, we then have this as


`=x^(-1/2)\left(-2a_1-6a_2x-10a_3x^2-14a_4x^3-18a_5x^4+\cdots\right)`

`=x^(-1/2)\displaystyle\sum_(n\ge1)(2-4n)a_nx^(n-1)`

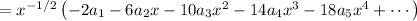
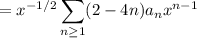
However I don't see the connection to the given answer... It seems some information is missing, specifically about how the coefficients
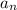
`a_n` are related.