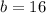Question

A painter leans a 20-ft ladder against a building. The base of the ladder is 12 ft from the building. To the nearest foot, how high on the building does the ladder reach?

Answer 1

Use Pythagorean Theorem.
a^2 + b^2 = c^2
Substitute the numbers.
12^2 + b^2 = 20^2
144 + b^2 = 400
Subtract 144 from each side.
b^2 = 256
Take square root.
The answer is
b = 16

Answer 2

The height of the building to which the ladder reaches is:

16 ft.

Explanation:

We can model this problem with the help of a right angled triangle ΔABC such that the hypotenuse of the triangle is 20-ft and one of it's leg is: 12 ft.

Now we are asked to find the other leg of the triangle.

We will use the Pythagorean Theorem in order to find the other leg.

Pythagorean Theorem says that: If c is the hypotenuse of the right triangle and a and b are it's two legs then,

`c^2=a^2+b^2`

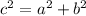
Hence, here we have:

`c=20,\ and\ a=12`

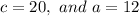
So,

`20^2=12^2+b^2\\\\i.e.\\\\400=144+b^2\\\\i.e.\\\\b^2=400-144\\\\i.e.\\\\b^2=256\\\\i.e.\\\\b=\pm 16`

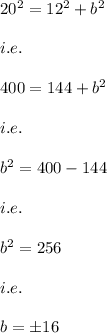
Since, b can't be negative as it denotes a side of a triangle.

Hence, we get:

`b=16`