Question

Trevor is analyzing a circle, y2 + x2 = 100, and a linear function g(x). Will they intersect?

Answer 1

yes, at positive x-coordinates

Answer 2

Given a circle described by the equation:

`y^2+x^2=100`
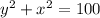
and a function g(x) given by the table

`\begin{center} \begin{tabular}c x & g(x) \\ -1 & -22 \\ 0 & -20 \\ 1 & -18 \end{tabular} \end{center}`

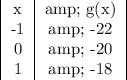
The function g(x) describes a straight line with the equation:

`(y-y_1)/(x-x_1) = (y_2-y_1)/(x_2-x_1) \\ \\ (y-(-22))/(x-(-1)) = (-20-(-22))/(0-(-1)) \\ \\ (y+22)/(x+1) = (-20+22)/(0+1) = (2)/(1) \\ \\ y+22=2(x+1)=2x+2 \\ \\ y=2x-20`

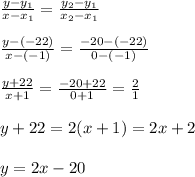
To check if the circle and the line intersects, we substitute the equation of the line into the equation of the circle to see if we have a real solution.
i.e.

`y^2+x^2=100 \\ \\ (2x-20)^2+x^2=100 \\ \\ 4x^2-80x+400+x^2=100 \\ \\ 5x^2-80x+300=0 \\ \\ x^2-16x+60=0 \\ \\ (x-6)(x-10)=0 \\ \\ x-6=0 \ or \ x-10=0 \\ \\ x=6 \ or \ x=10`

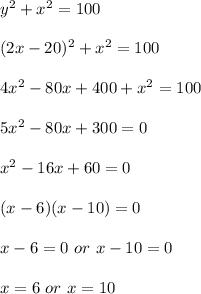
When x = 6, y = 2(6) - 20 = 12 - 20 = -8 and when x = 10, y = 2(10) - 20 = 20 - 20 = 0

Therefore, the circle and the line intersect at the points (6, -8) and (10, 0).