Question

there are 14 NBA teams who do not make the playoffs of these teams 3 of them will be randomly selected to make the 1st, 2nd, and 3rd pick. how many different ways can the 1st-3rd pick be arranged

Answer 1

the 1-3 picks could be arranged almost 25 different times 

Answer 2

In 2184 different ways can the 1st-3rd pick be arranged.

Explanation:

We are given the Total number of NBA teams does not make the play offs = 14

We need to find number of ways in which 3 teams randomly picked.

We use permutation to find the number of ways.

We know that number of ways of selecting r item from n different item is equal to
`^nP_r\:\:=\:\:(n!)/((n-r)!)`

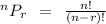
Here, r = 3 and n = 14

`\implies^(14)P_3=(14!)/((14-3)!)frac{14!}{11!}=frac{14*13*12*11!}{11!}=14*13*12=2184`

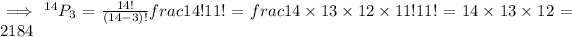
Therefore, In 2184 different ways can the 1st-3rd pick be arranged.