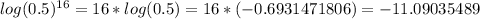Answer:
You mean ?

or
You mean?
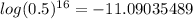
Explanation:
If you trying to solve:
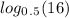
Then use the definition of the base of a log which is:
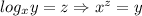
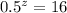
Rewrite 0.5 as:

As you may know:
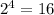
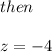
Let's use the negative exponent propierty in order to verify the result:
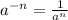
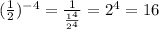
If you trying to solve:

Then use reduction of power propierty:
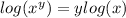
Therefore: