Question

Express in logarithmic form for the base. x y = P

Answer 1

so


`x^y=P`

remember

`a^b=c` translates to
`log_a(c)=b`
basically, the power that a must be raised to to obtain c is b

so

`x^y=P` translates to
`log_x(P)=y`

Answer 2

`y=\text{log}_x(P)`

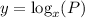
Explanation:

We are asked to write our given exponential equation
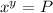`x^y=P` as logarithmic form.

First of all, we will take logarithm of both sides of our equation.

`\text{log}(x^y)=\text{log}(P)`

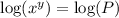
Using logarithm property
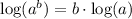`\text{log}(a^b)=b\cdot \text{log}(a)` we will get,

`y\cdot \text{log}(x)=\text{log}(P)`

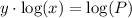
Dividing both sides by
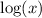`\text{log}(x)`, we will get:

`\frac{y\cdot \text{log}(x)}{ \text{log}(x)}=\frac{\text{log}(P)}{ \text{log}(x)}`

`y=\frac{\text{log}(P)}{ \text{log}(x)}`

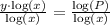
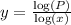
Using property
`\frac{\text{log}_x(a)}{\text{log}_x(b)}=\text{log}_b(a)`, we will get,

`y=\text{log}_x(P)`

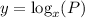
Therefore, our required expression would be
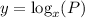`y=\text{log}_x(P)`.