Solution:
In the given function b(t), the variable t represents the number of years after 2008. The domain of this function is
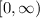 . The range more than 258.7 would not make sense. The graph of the function is always continuous.
. The range more than 258.7 would not make sense. The graph of the function is always continuous.
Step-by-step explanation:
The given function b(t) shows the population of bobcats in northern Arizona since 2008. Therefore the variable t represents the number of years after 2008.
Since t represents the number of years after 2008, which is either positive or zero, therefore the domain of this function is
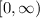 .
.
The given function is a quadratic function and the coefficient of
 is negative, so it is a downward parabola. The range above the y-coordinate of the vertex doesn't make any sense.
is negative, so it is a downward parabola. The range above the y-coordinate of the vertex doesn't make any sense.
The vertex of parabola is defined by
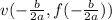 .
.
Vertex of the given function is (4.2,258.7).
Thus, the range more than 258.7 would not make sense for this function.
Since the given function is a polynomial function and polynomial functions are always continuous, therefore the graph of the function is always continuous.