Question

Convert the complex number into its polar representation: -4

Answer 1

check the picture below

Answer 2

`z= -4 ( cos \pi + i sin \pi)`

Explanation:

Complex number
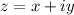`z= x+iy` can be written as follows

`z=r(cos \theta +i sin\theta )`

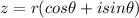
where
`r= \sqrt{x^(2)+ y^(2) }`

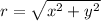
and
`\theta = tan^(-1) ((y)/(x) )`

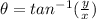
We have complex number
`z= -4`

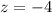
This can also be written as
`z= -4+i 0`

let us compare
`z= -4+i 0` with
`z= x+iy`

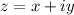
so we have
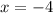`x= -4` and
`y= 0`

now we can find
`r` and
`\theta` in following ways

`r= \sqrt{(-4)^(2)+0^(2)}= -4`

`\theta = tan^(-1) ((0)/(-4)) =tan^(-1)(0)`

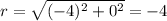
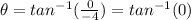
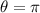`\theta = \pi` ( since x is negative so we take π )

now we have polar representation given by

`z= -4 ( cos \pi + i sin \pi)`