Question

Which set of ordered pairs represents a function?

{(2, –2), (1, 5), (–2, 2), (1, –3), (8, –1)}
{(3, –1), (7, 1), (–6, –1), (9, 1), (2, –1)}
{(6, 8), (5, 2), (–2, –5), (1, –3), (–2, 9)}
{(–3, 1), (6, 3), (–3, 2), (–3, –3), (1, –1)}

Answer 1

the one that doesn't have an "x" repeated, that is an X-REPEAT
notice, the pair is just an x,y pair.. .so if the "x" is repeated, is NOT a function

let's see


`\bf \{(2, -2), (\boxed{1}, 5), (-2, 2), (\boxed{1}, -3), (8, -1)\}\impliedby \textit{has an`

Answer 2

The second set of ordered pairs :

{(3,-1),(7,1),(-6,-1),(9,1),(2,-1)}

Explanation:

A function in IR2 (coordinate plane) assigns to a value of ''x'' an unique value of ''y''.

For example, the function
`f(x)=x+3`.

When
`x=2` ⇒
`f(2)=2+3=5`

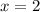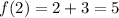
Therefore, the ordered pair
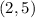`(2,5)` belongs to the function.

For each value of ''x'' we will have an unique value of ''y''.

For example, the ordered pairs
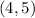`(4,5)` and
`(4,8)` don't belong to any function because the value ''4'' can't be assign to ''5'' and ''8'' at the same time.

On the other hand, we can have the same value of ''y'' assigns to different values of ''x''. For example ,
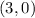`(3,0)` and
`(7,0)` are correct ordered pairs for the function
`y=0`.

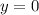In order to answer the question, we will discard the sets in which two or more ordered pairs have the same value of ''x'' assign to a different value of ''y''.

Examining the sets we find that the first set has the ordered pairs
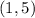`(1,5)` and
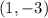`(1,-3)` so it is not a valid set of ordered pairs which represents a function.

The second set is correct.

The third set has
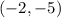`(-2,-5)` and
`(-2,9)` so it doesn't represent a function.

We will have the same problem in the fourth set with the ordered pairs
`(-3,1)` ,
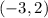`(-3,2)` and
`(-3,-3)`.

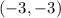The only correct set is the second one.