Question

Among all pairs of numbers whose difference is 18, find a pair whose product is as small as possible. What is the minimum product?

Answer 1

Answer: The minimum product is -81.

Explanation:

Let the larger number is x,

Then the smaller number will be (x-18) ( because the sum of these number is 18)

Hence, the product of these numbers,

f(x) = x(x-18)

⇒
`f(x) = x^2-18`

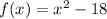
By differentiating with respect to x,

f'(x) = 2x - 18

For maxima or minima,

f'(x) = 0

⇒ 2x - 18 = 0

⇒ 2x = 18

⇒ x = 9

Again differentiating f'(x) with respect to x,

We get, f''(x) = 2

At x = 9, f''(x) = Positive

Hence, for x = 9,

f(x) is minimum,

And, the minimum value of f(x) = f(9) = 9(9-18)=9(-9) = -81

Hence, the minimum product is -81.

Answer 2

`\bf a-b=18\implies a=18+b \\\\\\ \textit{now, their product is }f=a\cdot b\implies f(b)=(18+b)b \\\\\\ f(b)=18b+b^2 \\\\\\ \cfrac{df}{db}=18+2b\implies 0=18+2b\implies 0=9+b\implies \boxed{-9=b}`

so, that's our only critical point, run a first-derivative test on it, and you'll notice is a minimum