Question

Given ​ f(x) = x^2 + 14x + 40 ​. Enter the quadratic function in vertex form in the box. f(x)=

Answer 1

Answer: f(x)=(x+7)^2-9. I took the test, I hope this helps you.

Answer 2

Recall that the vertex form of a quadratic function (or parabolic function) is equal to


`f(x) = a(x - h)^(2) + k`

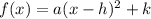
Now, given that we have f(x) = x² + 14x + 40, to express f into its vertex form, we must first fill in the expression to form a perfect square.

One concept that we must remember when completing the square is that

(a + b)² = a² + 2ab + b²

So, to complete the square for (x² + 14x + ____), we have 2ab = 14 where a = 1. Thus, b = 14/2 = 7. Hence, the last term of the perfect square must equal to 7² = 49.

So, going back to the function, we have


`f(x) = (x^(2) + 14x + 40 + 0)`

`f(x) = (x^(2) + 14x + 40 + 49 - 49)`

`f(x) = (x^(2) + 14x + 49) + 40 - 49`

`f(x) = (x + 7)^(2) - 9`

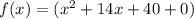
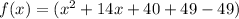
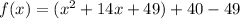
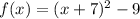
Thus, we have derived the vertex form of the function.

Answer: f(x) = (x + 7)² - 9