Let flower bouquet be
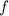
and vase be

Form two equations as follow
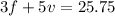
---> Equation 1
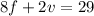
----> Equation 2
Using the elimination method:
Choose which variable, either
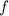
or

that we want to eliminate first. Say we choose

The next step is we need to make the constants of

to be the same value. At the moment we have
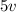
and
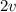
. Using the concept of common multiple, we will multiply
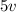
by
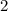
and the
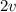
by 5 to get both

's with a constant 10
The rule of the Algebraic equation is: if we multiply one term by
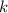
, then we need to do the same with all the other terms in the equations. So now we have
(
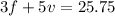
)×2 ⇒
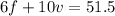
(
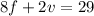
)×5⇒
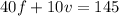
Now we can eliminate

by subtracting Equation 1 from Equation 2 (it would also work the other way around)
Equation 2 - Equation 1
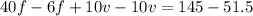
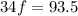
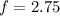
Now we've worked out the price of one flower bouquet, we can substitute back
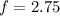
into either equation 1 or equation 2 to work out the price of one vase
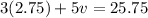

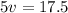
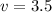
Hence, the price of one bouquet is $2.75 and one vase is $3.50