Question

what is the sum of a 7-term geometric series if the first term is -11, the last term is -45,056, and the common ratio is -4?

Answer 1

sn=(a1)((1-r^n)/(1-r))
=(-11)(1-(-4)^7)/(1-(-4))
=(-11)(1-(-16384))/5)
=(-11)(3277)
=-36047

Answer 2

The sum of a 7-term geometric series = -36047

Explanation:

We have 7-term geometric series if the first term is -11, the last term is -45,056, and the common ratio is -4.

So the GP is

-11, 44, -176,704,-2816,11264,-45056

Adding these terms we will get

Sum = -36047

Using equation:

We have

`s_n=(a(r^n-1))/(r-1)`

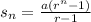
a = -11, r = -4 and n= 7

Substituting

`s_7=(-11((-4)^7-1))/(-4-1)=-36047`

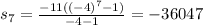
The sum of a 7-term geometric series = -36047