so hmmmmm, notice... the boat went up in 3hrs, came back to the starting point in 2hrs, it went up 108km, it came back, well, from 108km to distance 0, so the distance on the way back is just the same 108km
now... let's say the stream has a speed rate of "r", and the boat has a still water speed rate of "b"
bear in mind that, when the boat is going UP, is not really going "b" fast, because the stream's "r" rate is going against it, and thus subtracting "r" from "b", so is really going " b - r " fast
when the boat is going down, is not going "b" fast either, because, again the stream's rate "r" is adding to it, because is going with the current, so is really going " b + r " fast
now, recall your d =rt, distance = rate * time
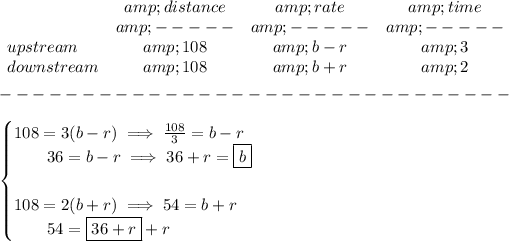
solve for "r"
what's b? well, 36+ r = b