Question

Does the following infinite series converge or diverge? 1/3+2/9+4/27+8/81+...

a. it diverges, it has a sum
b. it's converges, it has a sum
c. it diverges, doesn't have a sum
d. it converges, doesn't have a sum

Answer 1

Note that A and D are ludicrous choices, so you can throw them away outright. (Any divergent series cannot have a sum, and any convergent series must have a sum.)

The sum is certainly convergent because it can be written as a geometric sum with common ratio between terms that is less than 1 in absolute value.


`S=\frac13+\frac29+\frac4{27}+\frac8{81}+\cdots`

`S=\frac13\left(1+\frac23+(2^2)/(3^2)+(2^3)/(3^3)+\cdots\right)`

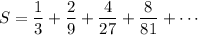
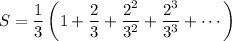
We can then find the exact value of the sum:


`\frac23S=\frac13\left(\frac23+(2^2)/(3^2)+(2^3)/(3^3)+(2^4)/(3^4)+\cdots\right)`


`\impliesS-\frac23S=\frac13`

`\implies\frac13S=\frac13`

`\implies S=1`

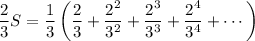
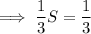
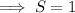
So the answer is B.