Question

Line segment ON is perpendicular to line segment ML, and PN = 10. what is the area of triangle MOL?

Answer 1

300

Explanation:

Answer 2

Given a circle with radius = 25 and the distance of the chord ML from the circumference = 10.
i.e. ON = 25 and PN = 10

But ON = OP + PN
25 = OP + 10

Thus OP = 25 - 10 = 15

Now to find the length of line segment MP, we note that triangle MOP is a right triangle with MO as the hypothenus.

MO is a radius to the circle, hence MO = 25 and OP = 15

Recall that the pythagoras rule for finding the length of the hypothenus says that the square of the length of the hypothenus is equal to the sum of the square of the lengths of the other two legs of a right triangle.

Thus,
`25^2=|MP|^2+15^2 \\ \\ |MP|^2=625-225=400 \\ \\ |MP|= √(400) =20`

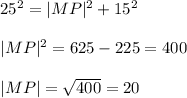
Recall that the area of a triangle is given by half of the base times the height.

Therefore, the area of triangle MOL is given by half ML times OP = MP times OP = 20 x 15 = 300 square units.