Question

Which set of numbers can represent the side lengths, in inches, of an acute triangle?

A 4, 5, 7
B 5, 7, 8
C 6, 7, 10
D 7, 9, 12

Answer 1

1. Let the sides of a triangle be a, b and c.

Assume c is the largest side.

The maximum angle measure in an acute triangle can be 90°. In such a case we would have
`a^(2) + b^(2) = c^(2)`

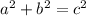
Now forget about side c, and open the angle between a and b just a little bit. Now clearly
`a^(2) + b^(2)` is larger that
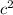
`c^(2)` because the "new c" is larger than the old one.

2. So for 3 numbers to be the lengths of the sides of an acute triangle, the sum of the squares of the 2 smaller numbers must be at most equal to the square of the largest number but not more.

Check:

A. 4^2+5^2=16+25=41<49
B. 5^2+7^2=25+49=74>64
C. 6^2+7^2=36+49=85<100
D. 7^2+9^2=49+81=130<144

3. Correct answer: only B