The volume of a cylinder is given by the formula V=(pi)(r^2)(h), where r is the radius of the cylinder and h is the height. Suppose a cylindrical can has radius (x + 8) and height (2x + 3). Which expression represents the volume of the can?
A)


+19

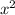
+112

x+192
B) 2


+35

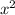
+80

x+48

C) 2


+35

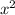
+176

x+192

B) 4


+44

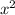
+105

x+72
