Question

A scientist measured the energy of a system and found that it was increasing. The data shown represent the energy taken every billionth of a second. Time (nanoseconds) 0 1 2 3 Energy (Joules) 2.654 6.290 14.909 35.335 Classify the type of growth the scientist observed.

Answer 1

Answer: exponential growth

Explanation:

From the given table, Energy taken by billionth in 1 sec
`E_1=2.654`

Energy taken by billionth in 2 sec
`E_2= 6.290`

Energy taken by billionth in 3 sec
`E_3= 14.909`

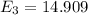
Energy taken by billionth in 4 sec
`E_4= 35.335`

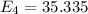
Now,
`(E_2)/(E_1)=(E_3)/(E_2)=(E_4)/(E_3)=2.37`

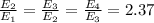
Since, they all have common ratio = 2.37

Hence there is a exponential growth of billionth.

[In exponential growth the ratio of the rate of change of the variable to its current size remains constant over time ]

Answer 2

At start ( t = 0 nanoseconds ) :
E ( t = 0 ) = 2.645 J
E ( t = 1 ) = 6.290 J
E ( t = 1 ) : E ( t = 0 ) = 6.290 : 2.645 = 2.37
Also:
E ( t = 2 ) : E ( t = 1 ) = 14.909 : 6.290 = 2.37
E ( t = 3 ) ; E ( t = 2 ) = 35.335 : 14.909 = 2.37
Therefore, the formula for calculating the energy of the system is:
E ( t ) = 2.645 * 2.37 ^ t
Answer: This is an exponential growth.