Answer:
25 g of an element will remain in the sample.
Step-by-step explanation:
Initial mass of an element =
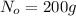
Final mass of an elemnt after time ,t = N
t = 30 days
Half life of an element =
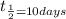
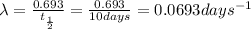
![\log[N]=\log[N_o]-(\lambda t)/(2.303)](https://img.qammunity.org/2018/formulas/chemistry/high-school/xwpufuef4n3hkfdn40isb1hq0tls7isu5k.png)
![\log[N]=\log[200 g]-(0.0693 days ^(-1)* 30 days)/(2.303)](https://img.qammunity.org/2018/formulas/chemistry/high-school/q0gfgs55mldibv9zyfxrrqtm5y2q7xfi7a.png)
N = 25.01 49 g ≈ 25 g
25 g of an element will remain in the sample.