1. The population of bacteria after time t, is given by the formula:
P(t)=
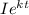
,
where I is the initial population and k the growth constant.
For example, the population at time t=0 is P(0)=
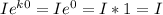
2.
P(t)=
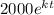
we can use the information we have:
P(4)=2,600=

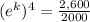

![e^(k)= \sqrt[4]{1.3} = \sqrt[2]{ \sqrt[2]{1.3} }= \sqrt[2]{1.14} =1.068](https://img.qammunity.org/2018/formulas/mathematics/high-school/q9c4sjzah7f3lf1h1qz61lw7h4ny3582lb.png)
3.
So the function becomes P(t)=
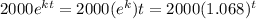
4. Population after 17 hours is P(17)=
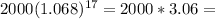
6120