Question

A 1.0 kg red superball moving at 5.0 m/s collides head-on with stationary blue superball of mass 4.0 kg in an elastic collision. What are the final velocities of the two superballs after the collision?

Answer 1

Initial conditions:
m1 = 1.0 ; v1 = 5
m2 = 4.0 ; v2 = 0

In the case where the second object (sometimes called the target) is at rest the velocities after the condition are

v1' = v1* (m1-m2)/(m1+m2)
v2' = 2v1*m1/(m1+m2)

For this we get
v1' = 5*(-3)/5 = -3m/s (moving in the opposite direction as before at 3m/s
v2' = 2*5*(1)/5 = 2m/s in the same direction as the original ball was moving
you can see these directions by looking at the signs. The momenta also add to the initial momentum as required.

Answer 2

final speed of blue ball = 2m/s

final speed of red ball = -3 m/s

Step-by-step explanation:

As we know that for elastic type of collision the coefficient of elasticity is always 1 and it is given by

`e = (v_2 - v_1)/(u_1 - u_2)`

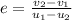
here we know that

`u_1 = 5 m/s`

`u_2 = 0`

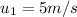
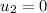
now we have

`v_2 - v_1 = 5 - 0 = 5 m/s`

also we can use the momentum conservation for this type of collision

so we will have

`1* 5 + 4 * 0 = 1* v_1 + 4 * v_2`

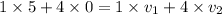
so we have

`v_1 + 4v_2 = 5`

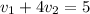
now from above two equations we will have

`5 v_2 = 10`

`v_2 = 2 m/s`

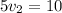
also we have

`v_1 = - 3m/s`

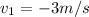
so final speed of blue ball = 2m/s

final speed of red ball = 3 m/s