Question

A penny dropped into a wishing well reaches the bottom in 1.50 seconds. What was the velocity at impact?

Answer 1

Assuming that it was dropped at an intital velocity of 0, 14.7s should be your ansewer

Answer 2

`-14.7 (m)/(s) \hat{j}`.

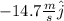Step-by-step explanation:

The kinematic equation for velocity
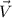`\vec{V}` with constant acceleration
`\vec{a}` at time t is :

`\vec{V}(t) \ = \ \vec{V}_0 \ + \ \vec{a} \ t`.

Assuming that the initial velocity is zero

`\vec{V}_0 = 0`

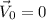
and knowing that the gravitational acceleration is

`\vec{a} = - 9.8 (m)/(s^2) \hat{j}`

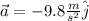
The equation is

`\vec{V}(t) \ =  - 9.8 (m)/(s^2) \ t \ \hat{j}`.

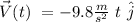After 1.5 seconds, this gives us

`\vec{V}(t) \ =  - 9.8 (m)/(s^2) \ t \ \hat{j}`.

`\vec{V}(1.5 s) \ =  - 9.8 (m)/(s^2) \ 1.5  s \ \hat{j} = -14.7 (m)/(s) \hat{j}`.

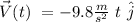And this is the velocity at impact.