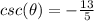Answer:
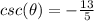
Explanation:
We've been told that θ terminates in Quadrant III, which means that θ is the angle between the positive x-axis and a vector
 with negative x and y coordinates.
with negative x and y coordinates.
Additionally, we know that
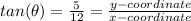
So, using this information we can conclude that:
x-coordinate=
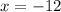
y-coordinate=
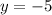
(This make sense because
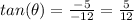 )
)
But, we still have to calculate
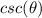

Where
 is the vector magnitude
is the vector magnitude
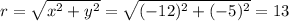

So we've found the answer: