Question

What are the x-intercepts of the function f(x) = –2x2 – 3x + 20?

Answer 1

The root sof this quadratic equation are -4 and 2.5.

The roots of any quadratic can be found by using the quadratic equation. The equation is below for you.

`\frac{-b +/- \sqrt{b^(2)- 4ac}}{2a}`

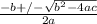
In this equation you use the number attached to x^2 as the a, which in this case is -2. The number attached to x as b, which is in this case -3. And the number at the end as c, which is 20. From there you solve for the answers.

`\frac{3 +/- \sqrt{-3^(2)- 4(-2)(20)}}{2(-2)}`

`(3 +/- √(9 + 160))/(-4)`

`\frac{3 +/- 13}}{4}`

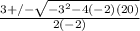
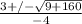
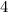
Now you separate and get the two separate answers. First the positive.

`\frac{3 + 13}}{4}`

`\frac{16}}{4}`

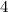
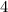
4

Now the negative

`\frac{3 - 13}}{4}`

`\frac{-10}}{4}`

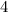
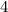
-2.5

Answer 2

Its A

Explanation:

I just took the test

OWO