Question

The angles of a triangle are in the ratio 11 : 5 : 2. The side opposite the largest angle is 5.5 centimeters. The length of the side opposite the smallest angle of the triangle is ? centimeters

Answer 1

2.00

mane trust me

Answer 2

The length of the side opposite the smallest angle of the triangle is 2 centimeter.

Explanation:

Given : The angles of a triangle are in the ratio 11 : 5 : 2. The side opposite the largest angle is 5.5 centimeters.

To find: The length of the side opposite the smallest angle of the triangle is?

Solution :

Let x be the angle of the triangle.

The angles of a triangle are in the ratio 11 : 5 : 2.

Sum of angles of the triangle is 180°.

So,
`11x + 5x + 2x = 180`

`18x = 180`

`x=10`

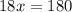
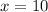
Therefore, The angles of the triangles are 110, 50,20 degrees.

Now, Applying Law of Sines:

i.e, to find the remaining sides of a triangle when two angles and a side are known we apply,

`(\sin A)/(a)=(\sin B)/(b)`

Let A=110°(as largest angle), a=5.5 cm(given)

B=20° (as 20 is the smallest angle), b=b(smallest length)

Substitute,

`(\sin 110)/(5.5)=(\sin 20)/(b)`

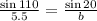
Cross multiply,

`b=(\sin 20* 5.5)/(\sin 110)`

`b=2.00`

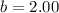
Therefore, The length of the side opposite the smallest angle of the triangle is 2 centimeter.