Question

thomas want to save money for a vacation. thomas invest 1,200 in account that pays an interest rate of 4% how many years will it take for the account to reach 14,400

Answer 1

Hi there
The formula is
A=p (1+r)^t
A future value 14400
P present value 1200
R interest rate 0.04
T time?
We need to solve for t
T=log (A/p)÷log (1+r)
So
T=log(14,400÷1,200)÷log(1+0.04)
T=63.4 years

Hope it helps

Answer 2

63.5 years take for the account to reach $ 14,400.

Explanation:

Given: Principal amount, P he invested in in account = $ 1200

Rate if interest , R = 4%

Amount, A = $ 14400

We need to find time in which principal amount reached to Amount.

We know that in banking sector Interest is compounded yearly.

So, We use compound interest formula and take n ( number of time interest applied ) = T ( time )

`A=P(1+(R)/(100))^T`

`14400=1200(1+(4)/(100))^T`

`12=((104)/(100))^T`

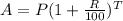
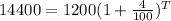
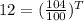
Taking log on both side,

`log\,12=log\,((104)/(100))^T`

`1.08=T(0.017)`

`T=(1.08)/(0.017)`

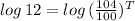
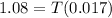
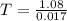
T = 63.5 years

Therefore, 63.5 years take for the account to reach $ 14,400.